Objekt des Monats Juli 2021
Eigentlich wollten wir aus dem Institut für Arbeits-, Sozial- und Umweltmedizin der FAU nur den NCR Decision Mate V
(Objekt des Monats Juni 2021) abholen.
Dabei kam beiläufig das Gespräch auf einen Karton mit alten medizinischen Geräten die zur Diagnostik verwendet wurden und die ebenfalls nicht mehr gebraucht und entsorgt werden sollten.
Darin fand sich neben einem Blutdruckmesser, Mikroskopen und weiteren uns nicht bekannten Geräten, ein Polarplanimeter.
Dieser „Beifang“ bei der Abholung des NCR, war ein Glücksfall für uns, da in der Abteilung 6 unserer Führungsline, den Analogrechnern, diverse Planimeter in einer Vitrine ausgestellt sind. Mit dem neu hinzu gekommenen Planimeter bietet sich nun die Möglichkeit die Funktionsweise dieser Analogrechner praktisch zu demonstrieren.
Unser Fundstück ist ein Polarplanimeter der Firma HAFF aus Pfronten im Allgaeu. Genauer; das HAFF 313E.
Obwohl die Technologie schon etwa 170 Jahre alt ist, werden Polarplanimeter noch immer genutzt und produziert.
Unser Exemplar ist etwa 35 Jahre alt. Das gleiche Modell gibt es bei HAFF für 549, noch immer neu zu erwerben.
Polarplanimeter werden dazu verwendet, Flächeinhalte zu bestimmen. Dazu fährt man mit dem
Fahrstift den Rand der zu messenden Fläche entlang.
Der Rand ist eine geschlossene Kurve, Anfangs und Endpunkt der Messfahrt ist derselbe. Das Vorzeichen der Messung wird dadurch bestimmt, ob der Rand im Uhrzeigersinn oder gegen den Uhrzeigersinn abgefahren wird.
Ein Planimeter ist also ein mechanisches Messgerät, das als mathematisches Instrument und Analogrechner, zur Ermittlung beliebiger Flächeninhalte in Landkarten oder Zeichnungen genutzt wird.
Die zu messenden Flächen können fast beliebige Form haben (unregelmäßige Polygone, andere unregelmäßige Flächen), müssen aber stetige und stückweise glatte Ränder haben. Die ganze Fläche muss in der Reichweite des Fahrarmes liegen, d. h. einen Durchmesser haben, der kleiner ist als das Doppelte der Fahrarmlänge (meist 20–30 cm). Die Genauigkeit liegt typischerweise bei ca. 1 ‰, bei speziellen Geräten auch höher.
Bild 1: Hier ein Beispiel: Bestimmung des Flächeinhaltes eines Burmester Kurvenlineals.
Wie ist ein Planimeter aufgebaut?
Das Bild oben zeigt die Kernbestandteile eines Polarplanimeters.
Die Bilder unten zeigen das Zählwerk mit dem Messrad, von oben und von unten gesehen.
Wie wird eine Messung durchgeführt?
Wenn es die Größe des zu messenden Objektes zulässt setzt man den Pol außerhalb des Objektes ab. Bei großen Objekten ist auch eine Messung mit im Objekt liegenden Pol möglich.
Der Untergrund auf dem das Messrad läuft sollte nicht zu rutschig sein und es sollten keine Übergangskanten zum Messblatt vorhanden sein an denen sich das Messrad verhaken kann.
Bild 1 zeigt das zusammengebaute Polarplanimeter. Der etwa 300 Gramm schwere Pol wird außerhalb der zu messenden Fläche abgelegt. Der Polarm verbindet, an beiden Enden drehend gelagert, den Pol mit dem Planimeter.
Zuerst wird grob die Messfläche umfahren um zu sehen, ob das Messrad frei und ohne Hindernisse laufen kann.
Vor der Messung ist aber noch die Einstellung des Fahrarms notwendig. Dies geschieht in dem man den Feststellhebel löst und den für seine Messung nötigen Wert durch Verschieben des Fahrarmes an der Anzeige einstellt.
Eine kleine Tabelle im Etui zeigt die gängigsten Einstellwerte. Für andere Maßstäbe gibt die Gebrauchsanweisung weitere Werte vor.
In unserem Fall haben wir keine Landkarte mit einem Maßstab vor uns, sondern eine Fläche, die 1:1, metrisch in cm2 gemessen werden soll.
Die Tabelle im Etui gibt dazu den Wert von 33,19 an.
Als Nächstes setzt man den Fahrstift mit der Lupe auf einen (markierten) Anfangspunkt der Messfläche und stellt mit dem Rückstellrädchen die Anzeigen auf „0“.
Die Messung geschieht im Uhrzeigersinn. Mit Daumen und Zeigefinger hält man die Lupe, deren Rand sich frei drehen kann, so dass mit den Fingern nicht umgegriffen werden muss.
Ein kleiner Ring in der Lupe gibt den Bezugspunkt zum Abfahren der Linie.
Die Abweichungen durch „zitteriges“ Umfahren der Linie gleichen sich in Etwa aus.
Ist der Startpunkt wieder erreicht, kann das Ergebnis an der Umdrehungsskala und an der Anzeige des Zählrades abgelesen werden.
Das Ergebnis ist immer 4stellig zu lesen. Die höchste Stelle ist die Anzeige der Umdrehungsskala.
Hier ist es die „1“.
Die Anzeige der 3. und 2. Stelle ist der Zahlenwert der Messradanzeige im Bezug zur „0“ des Nonius.
Hier ist es die „64“.
Die übereinstimmenden Striche des Nonius geben schließlich die erste Stelle des Ergebnisses an. Hier ist es die „1“.
Das abgelesene Ergebnis ist also die „1641“.
Aus der Tabelle ist ersichtlich, dass eine Einheit
als 0,1 cm2 interpretiert werden muss.
Die Gesamtfläche unseres Kurvenlineals beträgt also 164,1 cm2.
Um die reelle Fläche des Lineals zu erhalten müssen aber noch die beiden Ausschnitte gemessen und von der Gesamtfläche abgezogen werden.
Das Funktionsprinzip!
Das Funktionsprinzip beruht im Wesentlichen auf zwei mathematischen Prizipien:
1. Dem Satz von Green, der die Berechnung eines ebenen Flächenintegrals über das
Kurfenintegral einer stückweise stetig differenzierbaren Kurve gewährt. Daher genügt es tatsächlich nur den Rand einer solchen Fläche zu umfahren.
2. Das Prinzip der Berechnung infinitesimaler (ins unendlich Kleine gehende) Flächen nach Euler, das besagt, dass sich ein infinitesimales Flächenstück aus der Summe eines infinitesimalen
Parallelogrammes und einer infinitesimalen Dreiecksfläche zusammensetzt.
Das Planimeter ist also die technische Realisierung dieser beiden mathematischen Sachverhalte, wobei beim Umfahren einer gewünschten Fläche die Messeinrichtung infinitesimale kleine Flächen aufaddiert.
Dabei ist der zurückgelegte Weg des Messrades proportional zum Flächeninhalt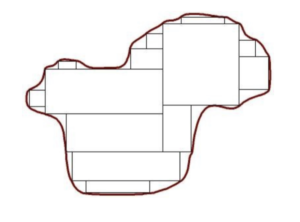 
der umfahrenenFläche. So dreht sich das Messrad nur in den wenigsten Fällen geradlinig in Längsrichtung, sondern schiebt sich proportional des senkrecht zurückgelegten Weganteils über die Oberfläche.
Bei einer axialen Verschiebung rutscht das Messrad lediglich über die Unterlage und dreht sich dabei nicht.
Praktischer Einsatz!
Die Bedienungsanleitung der Firma HAFF zeigt einige Anwendungsbeispiele auf.
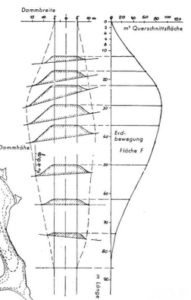
Im Tiefbau:
Um nötige Erdbewegungen zur Erstellung eines
Straßendammes zu bestimmen, oder
um den Wasserinhalt eines Speicherbeckens zu bestimmen.
Dabei werden zwei Flächenmessungen benoetigt.
Zuerst werden einige aus dem Kartenbild entnommene Querschnittsflächen berechnet und als Kurvenpunkte eingetragen.
Diese Kurvenpunkte werden dann miteinander verbunden und durch die zweite Flächenmessung dieses Graphs die Raummenge der benötigen Erde errechnet.
In der Biologie:
Zur Bestimmung der Assimilationsfähigkeit bei Wachstumsversuchen lassen sich Blattflächen ausmessen. Bei Mutationsuntersuchungen an Insekten können die Flügelflächen bestimmt werden. Bei der Entwicklung von Insektiziden können die Flächen von Fraßschäden an Blättern und in Geweben errechnet werden und bei der Chromatographie die Ausbreitung bestimmter Farbflächen im Testpapier.
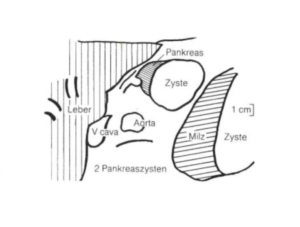
In der Onkologie:
Zur Bestimmung des lokalen Ansprechens von Hirntumoren auf Strahlentherapie. Hier werden Bilder einer Kernspintomographie vermessen.
Des weiteren besteht die Möglichkeit einer Quantifizierung des sogenannten perifokalen Ödems, einer Flüssigkeitsansammlung um den Tumor, die Ausdruck einer gestörten Bluthirnschranke ist.
Das letztgenannte Beispiel ist wahrscheinlich auch der Grund warum wir unser „Objekt des Monats Juli“ aus dem Fundus der Arbeitsmedizin bekommen haben.
Links:
https://www.didaktik.mathematik.uni-wuerzburg.de/history/ausstell/planimet/funktion.html
https://bluemich.net/rechner/rmplanimeter.htm
https://www.haff.de/mechanischeplanimeter
https://de.wikipedia.org/wiki/Planimeter
http://www.mathe.tufreiberg.de/~hebisch/cafe/seminarplanimeter.pdf